고정 헤더 영역
상세 컨텐츠
본문
2019년 3월 고2(가) 30번 문제입니다.
고등수학(하) 유리함수 문제가 질문으로 들어왔네요.
한 번 풀어보세요 ^^

풀이는 아래로 쭈욱~~~
많은 학생들이
합성함수가 포함된 문제들을 힘들어합니다.
처음 합성함수를 배웠을 때를 생각해 보면
이런 그림이 떠오를 겁니다.

위의 그림을 줄여서

결과만 보면 아래 것이 훨씬 간단하죠.
그런데 말입니다.
아래 것은 중간에 어떤 과정을 거쳤는지
무슨 일이 일어났는지 알 수가 없습니다.
간단한 것은 아래 것이지만,
정보를 온전히 가지고 있는 것은 위죠.
위의 그림을 그래프에 나타내 보겠습니다.


중간 과정에 무언가를 해석해야 한다면
어떤 것이 유용해 보이시나요?
너무 간단해서 차이를 못 느끼시겠다고요?
그럼 이건 어떨까요?
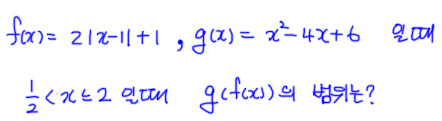
합성함수의 그래프를 그리겠다.(앞의 상황에서 아래경우)
저는 안 하겠습니다. 귀찮습니다.
대충 어떻게 진행이 되는 지만 설명하겠습니다.
1.
x가 0.5 초과 1이하인 범위와 1이상 2 이하인 범위로 나눠
f(x)를 나눠 절댓값을 없애줍니다.
2.
나눠진 f(x)를 g(x)의 x자리에 대입하여 합성함수를 구합니다.
대입하고, 전개하고, 정리해서 표준형 만들어야 합니다.
3.
합성함수 그래프를 범위에 따라서 점선으로 그립니다.
4.
x가 0.5초과 2이하 인 부분만 실선으로 그립니다.
5.
g(f(x))의 범위를 구합니다.
맨 마지막 단계에서 값을 대입하고
합성함숫값을 찾아내는 과정에서는 간단해 보이지만
합성합수를 찾는 과정이
그래프가 복잡하면 복잡할수록 쉽지 않습니다.
그럼, 이제 앞의 상황에서 위의 경우와 같이
그래프를 따로따로 그려볼까요?
전 개인적으로 이 방법을 좋아합니다.
이때 주의할 것은 축입니다. 축을 잘 보세요!

x의 값이 0.5에서 2까지 커짐에 따라
그래프는 점 A에서 점 B를 지나 점 C로 갑니다.
x가 0.5일 때 A, 이때 f(x)는 2, 점 D와 연결이 되겠죠?
x가 0.5에서 1로 가면 f(x)는 2에서 1로
x가 1이 되면 B, 이때 f(x)는 1, 점 E와 연결!
즉 좌측 그래프가 A에서 B로가면
우측 그래프는 D에서 E로 가네요.
좌측 그래프에서
x가 1에서 2로 변하면 ( B에서 C)
f(x)는 1에서 3으로 변하고, (E에서 F)
이렇듯 함수를 따로따로 그리고
그 연결 부분을 잘 파악하면
중간에 어떤 일이 벌어지는지까지 이해할 수 있죠.
자! 이제 원래 질문으로 돌아가 문제를 풀어볼까요?
근데 풀이가 길어질 것 같으니
여기까지 사전학습이었습니다. ^^
다음 글에서 계속..^^
진짜 수학을 만나다 : 네이버 블로그
원리와 개념에 맞게 생각하는 힘을 키우는 수학학원 상담문의 : 010-4626-0179 위치 : 복대동 지웰 시티 흥복드림몰 605호
m.blog.naver.com
'고등수학 > 고1' 카테고리의 다른 글
| [수1] 지수함수 - 정수점개수 (0) | 2023.11.09 |
|---|---|
| [고등(하)] 2019년 3월 고2(가) 30번 풀이 (1) | 2023.11.08 |
| [고등(하)] 순열과 조합 - 대진표 (3) | 2023.11.07 |
| [고등(하)] 순열과 조합 - 대진표 사전 학습 (1) | 2023.11.07 |
| [고등(하)] 순열과 조합 - 진열장 (1) | 2023.11.06 |




