[중1-1] 최대공약수와 최소공배수의 관계

36과 120의 최대공약수와 최소공배수를 아는가?

 

같은 방식으로

두 자연수 32와 N의 최대공약수가 16이고,

최소공배수가 96일 때, N을 구할 수 있는가?

 

---

아래로 쭈욱~~~~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

반응형

---

질문에 답을 하기 앞서서

우리가 먼저 배운 최소공배수를 구하는 법이

기억이 나지 않는다면 복습 먼저!

[중1-1] 공배수와 최소공배수, 최소공배수 구하기

 

 

자! 그럼 우선 36과 120이 어떤 수로 이뤄져 있는지

알아야 하니까 소인수 분해!

30과 120의 최대 공약수는

두 수를 모두 나눌 수 있는 수 중에서 가장 큰 수

(2를 2번까지, 3은 한 번까지 나눌 수 있음.)

 

30과 120의 최소공배수는

두 수에 각각 자연수를 곱해서 같아지는 수 중

가장 작은 수

최소공배수는

2를 최소 3번, 3은 최소 2번, 5는 최소 1번

곱해져 있어야

같은 방식으로

두 자연수 32와 N의 최대공약수가 16이고,

최소공배수가 96일 때, N을 구할 수 있는가?

 

N은 소인수분해를 할 수 없으니

최대공약수와 최소공배수를 보고 판단해 보자.

최대공약수를 보면

두 수를 최대한 2로 4번까지 밖에 못 나누니

N은 2가 4번 곱해져 있음을 알 수 있다.

 

최소공배수를 보면

두 수에 각각 자연수를 곱해서 같아지는 수 중

가장 작은 수인데,

최소공배수에는 3이 인수로 되어 있는데

32는 3을 인수로 가지지 못하므로

N에 3이 곱해져 있음을 알 수 있다.

 

따라서

 

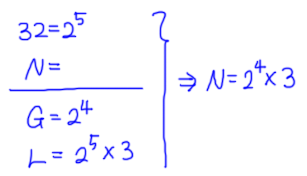
그럼 세 수일 때도 같은 방식으로 생각할 수 있나?

세 자연수 N, 12, 18의 최대공약수가 6이고,

최소공배수가 180일 때,

세 번째로 작은 자연수 N은?

 

일단 소인수분해!

일단 최대공약수를 보면,

세 수를 모두 2 한번, 3 한 번까지 나눌 수 있으므로

N은 2가 최소 1번 이상 곱해져 있음을 알 수 있고,

3도 최소 1번 이상 곱해져 있음을 알 수 있다.

 

최소공배수를 보면

각 수에 자연수를 곱해서 최소공배수가 되어야 하므로,

N은 2가 최대 2번, 3도 최대 2번,

최소공배수의 인수 5는 12와 18의 인수가 아니므로

N은 5가 한 번 곱해져 있어야 함.

 

N이 될 수 있는 모든 경우를 따져보면,

N = 30, 90, 60, 180

이 수 중에서 세 번째로 작은 수는? 90!

 

 

책에는 나오지만, 외울 필요는 없고,

두 수 사이에서만 쓸모가 있는 내용!

세 수 이상에서는 쓸모가 없음!

 

36과 120의 최소공배수를 구한다고 생각을 해보면

소인수분해를 해서 보면

각 수에 자연수를 곱해서

두 수를 같게 만드는 것이므로,

이미 서로 공통적으로 가지고 있는 수들이 아닌

서로 겹치지 않는 수들만 서로 바꿔서 곱하면

같아지지 않는가 라는 생각에서

소인수분해한 식을 다르게 정리해 보면

36에는 2와 5를 곱하고,

120에는 3을 곱해주면

최소공배수가 됨을 알 수 있다.

이걸 문자로 나타내 보면

최소공배수는

두 수를 곱하고 최대공약수로 나눔

다르게 말을 하면

두 수의 곱과

최대공약수, 최소공배수의 곱이 같다.

그런데, 이건 두 수 사이에서나 써먹을 수 있음.

세 수 이상의 수 사이에서는 쓸모가 없음.

 

그냥 이런 것도 있다 정도만 알아두고,

앞에서 쓰인

최대공약수와 최소공배수를 보고 해석하자!

 

진짜 수학을 만나다 : 네이버 블로그