[중2-2] 내접원과 내심

한 다각형의 내접원과 내심에 대해서 설명할 수 있는가?

​모든 다각형은 내접원이 존재하는지 그렇지 않은지 설명할 수 있는가?

---

아래로 쭈욱 ~~~

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

반응형

---

내접원 : 한 다각형의 모든 변에 접하는 원

​내심: 내접원의 중심

​

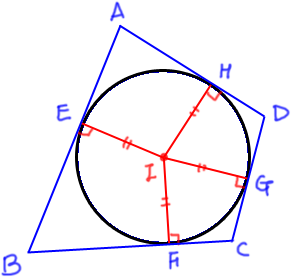
위의 그림은 사각형 ABCD의 내접원을 그린 것이다.

위의 그림에서 보듯이 선분 IE, IF, IG, IH가 모두 같다.

​그럼 내접원의 중심인 내심 I를 찾기 위해서 우린 어떻게 해야할까?

선분 IE와 IF가 같다는 말은

점I가 변 AB와 변 BC 에서 같은 거리에 있다는 말이고

이는 점I가 각 ABC의 이등분선 위에 있다는 말이 된다. (참고)

마찬가지로 점 I는 모든 각의 이등분선 위에 있어야 한다.

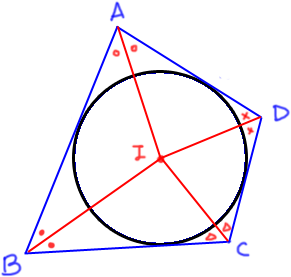
모든 각의 이등분선이 한 점에서 만나게 되면

그 다각형은 내접원이 존재하는 것이고,

모든 각의 이등분선이 한 점에서 만나지 않게 되면

그 다각형은 내접원이 존재하지 않게 되는 것이다.

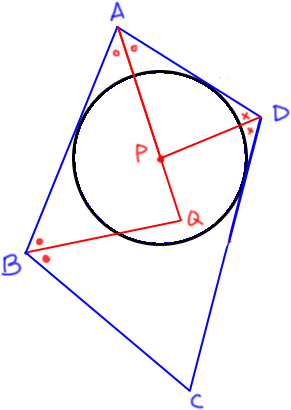
이 그림에서

점 P는 변 AB, 변 AD, 변 CD에 이르는 거리가 같은 점이고,

점 Q는 변 AB, 변 AD, 변 BC에 이르는 거리가 같은 점이다.

점 P에서 변 BC 까지의 거리는 나머지 세 변까지 이르는 거리와 같지 않고,

점 Q에서 변 CD 까지의 거리는 나머지 세 변까지 이르는 거리와 같지 않다.

즉 네 변에 이르는 거리가 같은 점은 존재하지 않는다.

위에 있는 사각형 ABCD는 내접원이 존재하지 않는다.

​

삼각형의 경우에는 무조건 내내접원이 존재하고,

삼각형을 제외한 다른 다각형의 경우에는 내접원이 존재할 수도, 존재하지 않을 수도 있다.

---

 

[중2-2] 각의 이등분선의 성질 (not in 삼각형)

 

진짜 수학을 만나다 : 네이버 블로그